Dijkstra Vs The New Deterministic Sssp Algorithm: Easy Guide, Php Examples, And Visuals
Last updated on
TL;DR
- Dijkstra’s algorithm is the classic way to compute shortest paths with non-negative weights, running in about O(m + n log n).
- A 2025 result gives a deterministic SSSP for directed graphs that runs in O(m · (log n)^(2/3)) in the comparison-addition model. It beats the long-standing n log n “sorting barrier” on sparse graphs.
- Big idea in plain words: instead of strictly sorting by distance at every step like Dijkstra, the new method processes nodes in smart batches using bounded multi-source relaxations and a reduced frontier of pivots.
The problem in one minute
Single-Source Shortest Path (SSSP) asks: given a source node, what is the minimum distance to every other node in a weighted graph. Classic answer: Dijkstra’s algorithm for non-negative weights. It repeatedly picks the closest unfinished node, then relaxes its outgoing edges. That “pick the closest” step creates a sorting-like cost of about log n per operation, which is why the total time has the n log n behavior.
Researchers showed a new deterministic way that reduces the dependency on sorting by exploring nodes in layers and shrinking the active frontier so heavy work applies only to a small subset. This changes the asymptotic behavior to O(m · (log n)^(2/3)).
Visuals to anchor the intuition
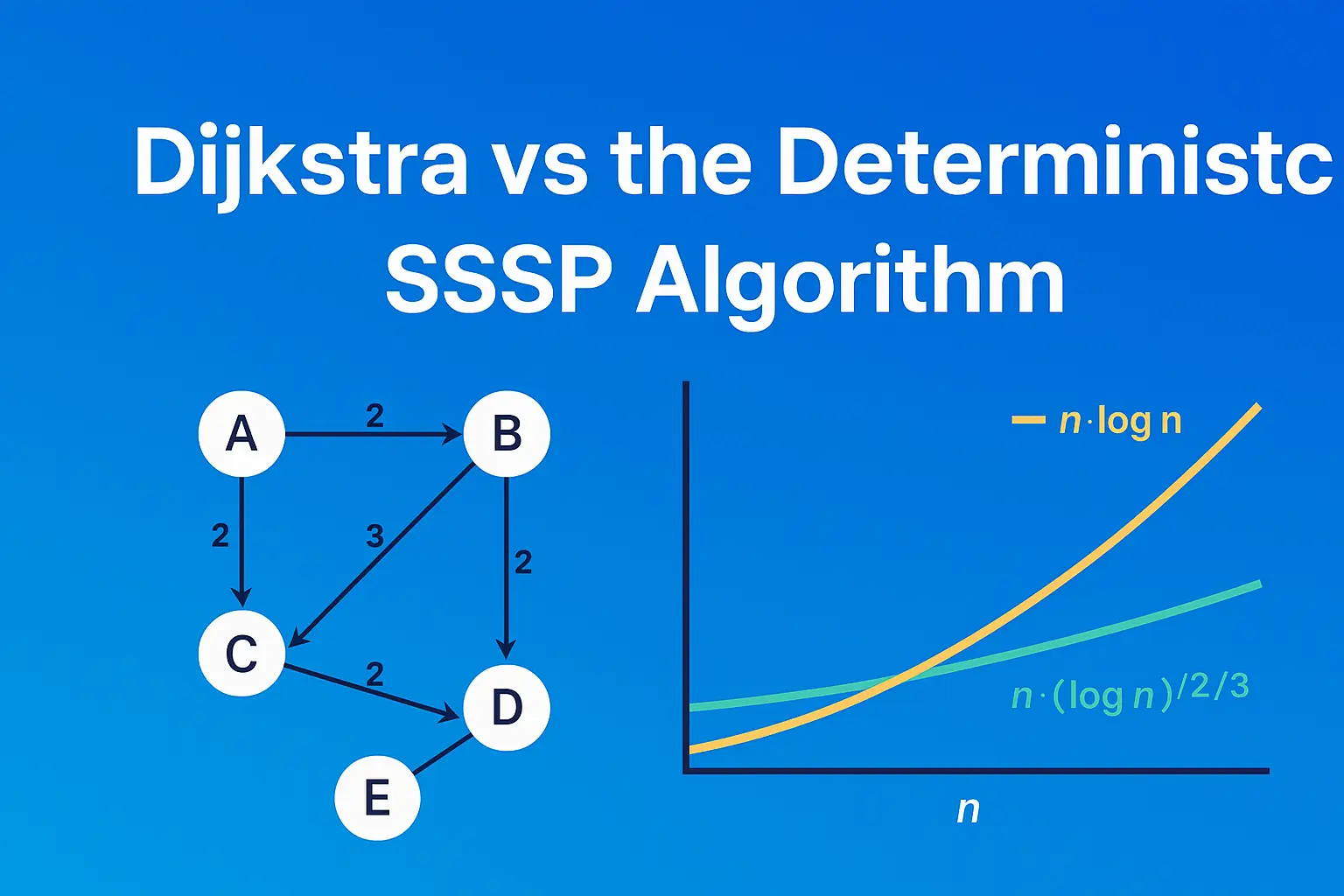
1) Growth trend: n·log n vs n·(log n)^(2/3)
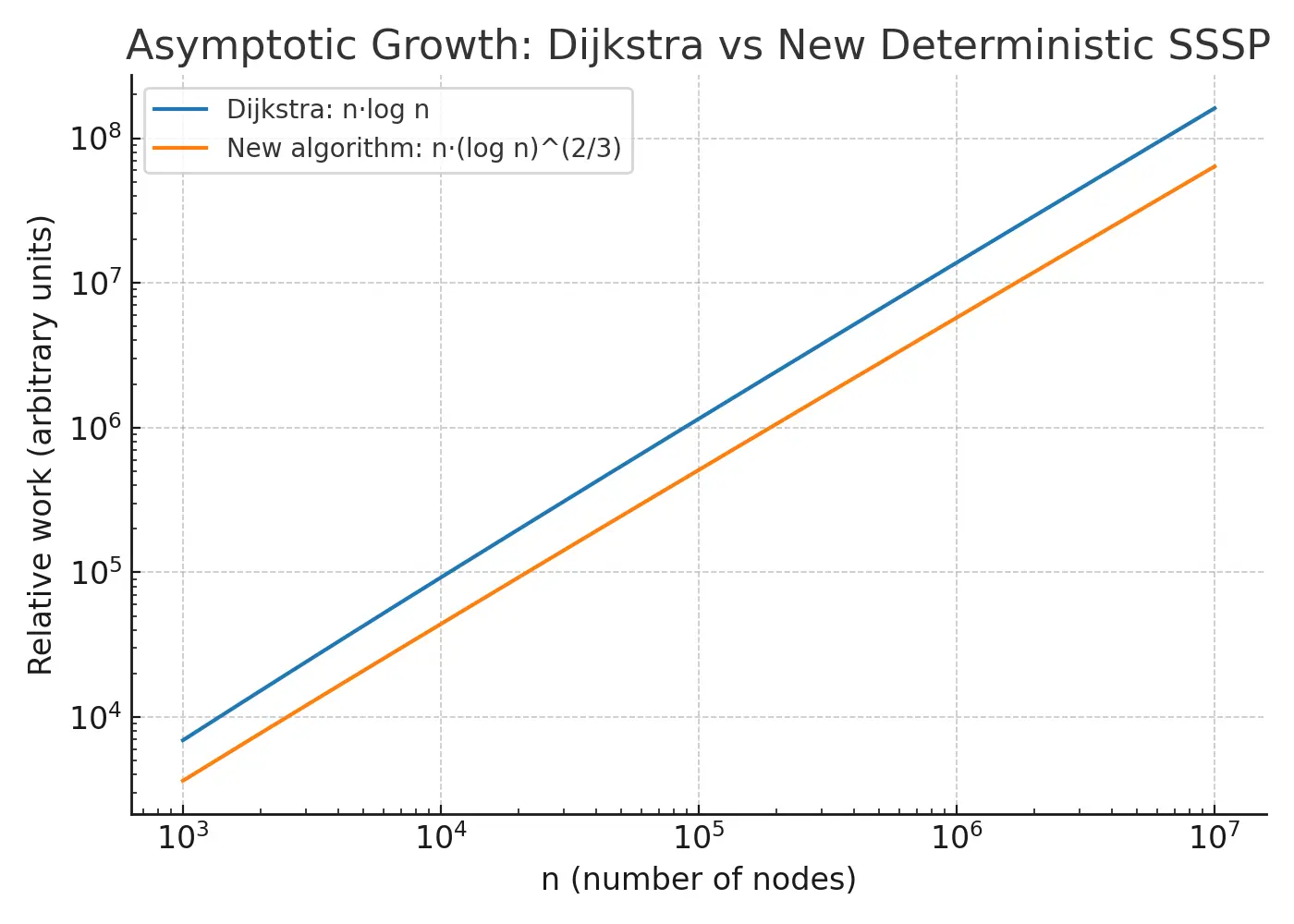
What you see: both grow with n, but n·(log n)^(2/3) grows a bit slower than n·log n. For huge graphs, that gap matters.
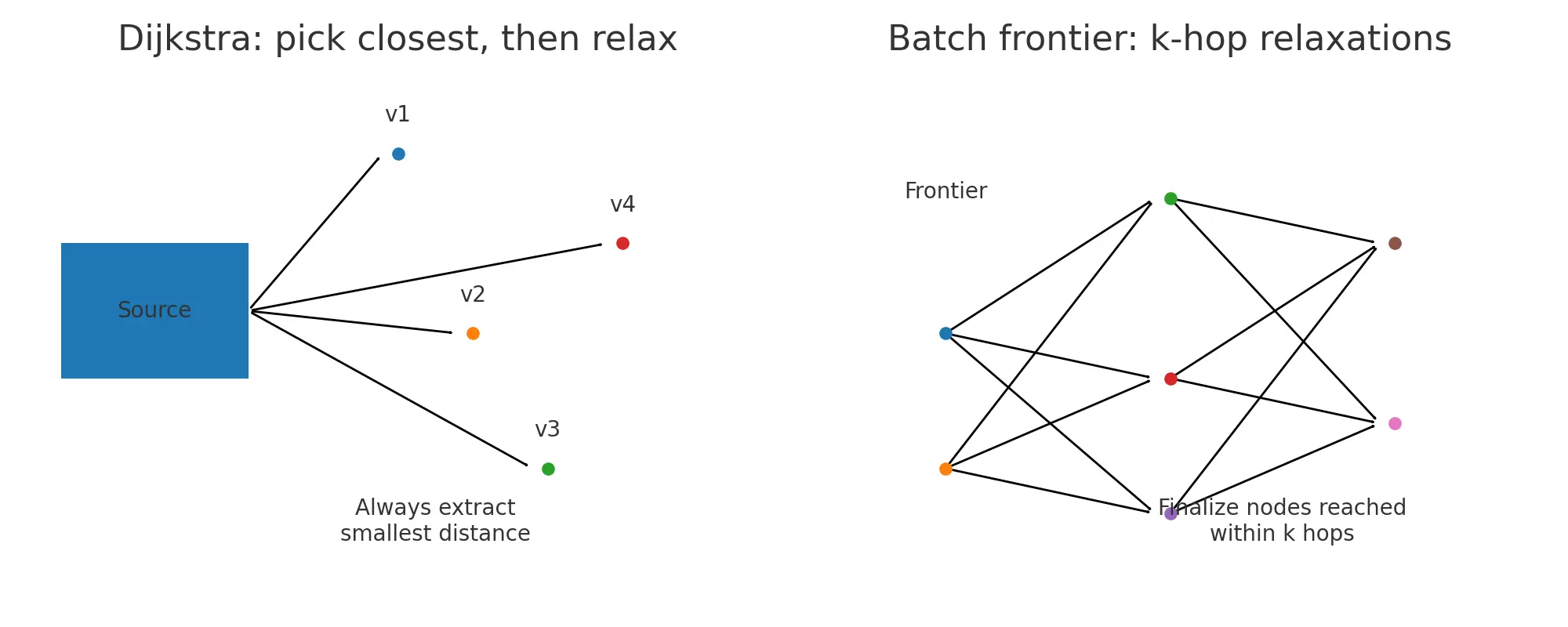
2) What changes operationally
Left: Dijkstra picks exactly the closest next node each step. Right: the new mindset processes a batch frontier and runs a few k-hop relaxations, then moves the frontier forward.
3) Tiny graph we will use in code
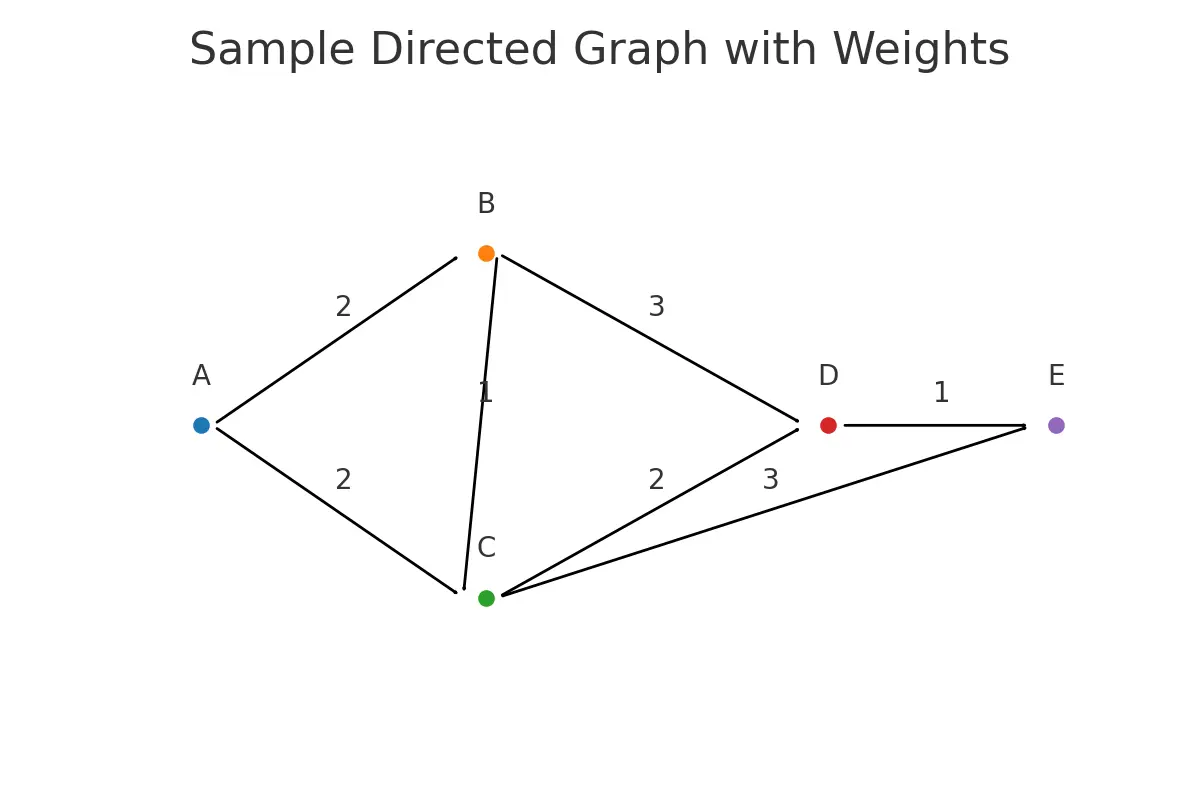
Edges: A→B(2), A→C(2), B→C(1), B→D(3), C→D(2), C→E(3), D→E(1) Expected distances from A: A 0, B 2, C 2, D 4, E 5
Practical example 1: Dijkstra in PHP
This is a clean, didactic version. It uses a simple linear scan for the minimum to keep it readable. For production, use a binary heap or Fibonacci heap.
1// Dijkstra's Algorithm — simple, highly commented version 2$graph = [ 3 'A' => ['B' => 2, 'C' => 2], 4 'B' => ['C' => 1, 'D' => 3], 5 'C' => ['D' => 2, 'E' => 3], 6 'D' => ['E' => 1], 7 'E' => [] 8]; 9 10$source = 'A';11$INF = 1_000_000;12 13// 1) Distance init14$dist = [];15foreach ($graph as $node => $_) $dist[$node] = $INF;16$dist[$source] = 0;17 18// 2) Finalized set19$visited = [];20 21// 3) Repeatedly extract the closest unvisited node and relax edges22while (count($visited) < count($graph)) {23 // extract-min24 $minNode = null; $minDist = $INF;25 foreach ($dist as $node => $d) {26 if (!isset($visited[$node]) && $d < $minDist) {27 $minDist = $d; $minNode = $node;28 }29 }30 if ($minNode === null) break; // no more reachable nodes31 32 // finalize33 $visited[$minNode] = true;34 35 // relax neighbors36 foreach ($graph[$minNode] as $nbr => $w) {37 if (!isset($visited[$nbr])) {38 $alt = $dist[$minNode] + $w;39 if ($alt < $dist[$nbr]) $dist[$nbr] = $alt;40 }41 }42}43 44// 4) Print45echo "Dijkstra distances from $source:\n";46foreach ($dist as $node => $d) echo "$node: $d\n";What to notice
- The algorithm always orders the frontier to pick the absolute smallest.
- That global ordering is where the log n overhead comes from.
Practical example 2: Batch-style deterministic idea in PHP
The full research algorithm is involved. The script below captures the core flavor: limited-depth relaxations from a frontier as a batch, then move the frontier forward. It avoids a global extract-min. It is meant for learning and mirrors the high-level design decisions.
1// Batch-style multi-source relaxations — educational approximation 2$graph = [ 3 'A' => ['B' => 2, 'C' => 2], 4 'B' => ['C' => 1, 'D' => 3], 5 'C' => ['D' => 2, 'E' => 3], 6 'D' => ['E' => 1], 7 'E' => [] 8]; 9 10$source = 'A';11$INF = 1_000_000;12 13// Distances14$dist = [];15foreach ($graph as $node => $_) $dist[$node] = $INF;16$dist[$source] = 0;17 18// Limit per batch — think "k-hop" relaxations19$k = 2;20 21// Start from the source frontier22$frontier = [$source];23$changed = true;24 25while ($changed) {26 $changed = false;27 28 // If frontier is empty but improvements may exist, restart from all nodes29 if (empty($frontier)) $frontier = array_keys($graph);30 31 // Track nodes improved in this batch32 $touched = [];33 34 // Up to k layers from current frontier35 $wave = $frontier;36 for ($round = 1; $round <= $k; $round++) {37 $nextWave = [];38 foreach ($wave as $u) {39 foreach ($graph[$u] as $v => $w) {40 $alt = $dist[$u] + $w;41 if ($alt < $dist[$v]) {42 $dist[$v] = $alt;43 $touched[$v] = true;44 $nextWave[] = $v;45 $changed = true;46 }47 }48 }49 if (empty($nextWave)) break;50 $wave = $nextWave;51 }52 53 // New frontier only where progress happened54 $nextFrontier = [];55 foreach (array_keys($touched) as $u) {56 foreach ($graph[$u] as $v => $_w) $nextFrontier[$v] = true;57 }58 $frontier = array_keys($nextFrontier);59}60 61// Print62echo "Batch-style distances from $source:\n";63foreach ($dist as $node => $d) echo "$node: $d\n";What to notice
- No priority queue.
- Work happens in short waves from a reduced frontier, not by a global strict order every step.
- This matches the paper’s idea of bounded multi-source relaxations and frontier reduction, without reproducing all the complexity.
Why the new idea helps
Dijkstra pays a log n cost in selecting the next node because it maintains a full order of candidate distances. The new method avoids that by:
- grouping work into batches,
- limiting relaxations to k layers per batch,
- shrinking the frontier to a small set of pivots before recursing. This breaks the sorting bottleneck and yields O(m · (log n)^(2/3)) time.
Complexity comparison
| Algorithm | Works on | Idea in one line | Time complexity |
|---|---|---|---|
| Dijkstra | Non-negative weights | Always extract the closest unfinished node, then relax | O(m + n log n) in comparison-addition model |
| New deterministic SSSP | Directed, non-negative weights | Batch relaxations from a reduced frontier with recursion and pivots | O(m · (log n)^(2/3)) |
Rule of thumb
- Small or medium graphs: Dijkstra is simple and often fast enough.
- Very large directed graphs: the new approach has better asymptotic behavior and is theoretically faster.
FAQ
Does the new algorithm replace Dijkstra in everyday code Not necessarily. Dijkstra is simple and widely available. The new method is deeper and shines at scale.
Can the new idea handle negative weights The result is for non-negative weights in the comparison-addition model. Negative weights are a different problem with separate lines of research.
Final takeaways
- Dijkstra remains a practical baseline for non-negative weights.
- The 2025 deterministic SSSP shows we can beat the classic n log n barrier by changing how we explore the frontier. It uses bounded multi-source relaxations, a shrunken frontier, and recursion to avoid repeated global sorting.
If you need an engineer who can translate advanced algorithmic ideas into production-ready systems with clean PHP and JavaScript, integrate complex SaaS APIs like HubSpot or Salesforce, design scalable architectures, and lead teams with DevOps discipline, I would love to help. I have 13+ years of experience across PHP, Laravel, Node.js, MySQL, PostgreSQL, and modern frontend stacks, plus deep integration work with NetSuite, SAP, and Shopify. I build maintainable code, robust pipelines, and clear documentation. Let us discuss your project. You can reach me through my Upwork profile.